技術談話

[話題7]　膨張畳込みと文脈情報の多重化について

　コンピュータビジョンにおける多くの問題は濃密予測の範疇に入る事例です。 その最終目標は、画像の各画素に対する離散的あるいは連続的なラベルを求めること、 すなわちセマンティックセグメンテーションを行うことです。 セマンティックセグメンテーションを行う最新のネットワークモデルでは、畳込みネットワーク(CNN)を 適応的に利用しています。 しかしながら、CNNはもともと画像分類のために設計されたものであるため、 セマンティックセグメンテーションのような濃密予測問題には、 必ずしも構造的に適しているとは言えません。 そこで、濃密予測に特化した新しい畳込みネットワークモジュールが考え出されました。 そのモジュールでは、 膨張畳込み(Dilated Convolution、あるいは Atrous Convolution)を使って、 多重スケールでの情報を解像度を下げることなくシステマティックに集めることができます。 この機構は、膨張畳込み処理が解像度や対象域を失うことなく受容野を指数関数的に 拡大するという事実を拠り所にしています。

膨張畳込み(Dilated Convolutions)

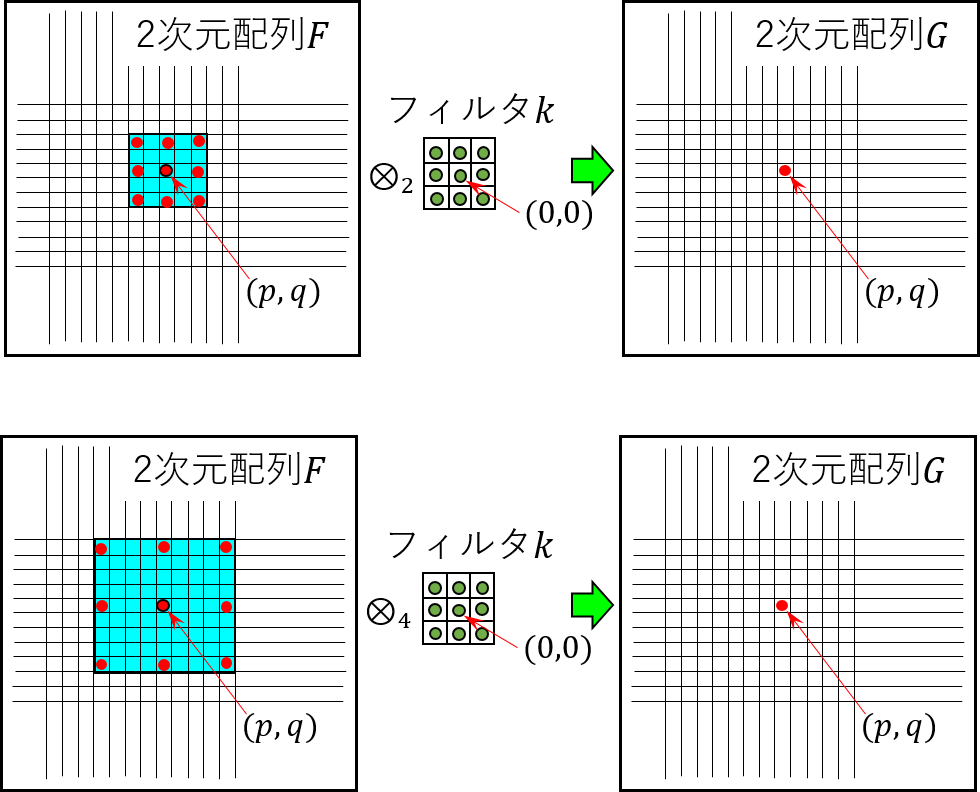
$F:\Bbb {Z^2}\rightarrow \Bbb{R}$を離散関数、$\Omega_r=[-r,r]^2\cap \Bbb{Z^2}$とし、 $k:\Omega_r\rightarrow \Bbb{R}$を$(2r+1)\times (2r+1)$の大きさの離散フィルタとするとき、 離散畳み込み演算子$\otimes$は以下の様に表されます。 \begin{equation} G(\boldsymbol p)=(F \otimes k) (\boldsymbol p) = \sum_{\boldsymbol{s+t=p}} F(\boldsymbol s)k(\boldsymbol t). \end{equation} この式表現から畳込み処理をイメージすることが難しい場合は、$\boldsymbol{s = p-t}$として 以下の様に表現し直すと良いかもしれません。 \begin{equation} G(\boldsymbol p)= \sum_{\boldsymbol t}F(\boldsymbol{p-t})k(\boldsymbol t) \\ \end{equation} さらに、入出力の位置ベクトルを2次元座標系の $\boldsymbol p =(n_1,n_2),\boldsymbol t=(m_1,m_2)$ で表すと、通常用いられる離散系の畳込み演算を表す式が得られます。 \begin{equation} G(n_1,n_2) = \sum_{m_1=-r}^{r}\sum_{m_2=-r}^{r}F(n_1-m_1,n_2-m_2)\cdot k(m_1,m_2) \end{equation}

続いて、ある正の整数$l$を用いて上式の畳込み演算を一般化します。すなわち、 \begin{equation} (F \otimes_l k)(\boldsymbol p) = \sum_{\boldsymbol s + l\boldsymbol t = p} F(\boldsymbol s)k(\boldsymbol t) \end{equation} この式を前述の畳込み演算の表現式で表すと以下の様になります。 \begin{equation} G(n_1,n_2) = \sum_{m_1=-r}^{r}\sum_{m_2=-r}^{r}F(n_1-l\times m_1,n_2-l\times m_2) \cdot k(m_1,m_2) \end{equation} 積和演算変数$m_1$と$m_2$に関して、関数$F$とフィルタ$k$のドメインの変位量に注目すると、 フィルタ$k$においては変数の変位量に応じたフィルタ係数が取り出されますが、関数$F$に対しては、 変数$m_1$と$m_2$それぞれ$l$倍された変位量の位置での関数値が参照されることを示しています。 関数$F$を2次元座標上に配置された画像と考え、膨張畳込み処理の概念を図として表したのが、次の 図6-1です。$F$を入力画像、$k$を$3\times 3$のフィルタとし、$\otimes_2$と$\otimes_4$ の膨張畳込み処理において、ある点$(p,q)$での畳込み計算結果を求める流れを表しています。 $F$中の水色矩形領域が受容野を表し、受容野中の各赤丸点とフィルタの対応する各係数との積和が $G$中の$(p,q)$座標に格納されます。式ではそれぞれ、以下の様に表されます。ただし、入力画像 については右下端を原点とし、上および左方向を正の向きとする座標系、フィルタについては フィルタ中心を原点に右および上方向を正の向きとする座標系とします。パラメータ$l$は膨張係数 と呼ばれています。膨張係数を大きくしていくと、入力配列に対する受容野が指数的に増大していくことが 分かります。すなわち、同じフィルタに対して積和を取る2次元配列の要素の位置が広がっていきます。

図7-1 膨張畳込み処理の概念図
\begin{equation} G(p,q) = \sum_{m_1=-1}^{1}\sum_{m_2=-1}^{1}F(p-2\times m_1,q-2\times m_2) \cdot k(m_1,m_2) \label{eq:7-6} \end{equation} \begin{equation} G(p,q) = \sum_{m_1=-1}^{1}\sum_{m_2=-1}^{1}F(p-4\times m_1,q-4\times m_2) \cdot k(m_1,m_2) \label{eq:7-7} \end{equation} 図7-1の２つの畳込みを式で表したものが式(\ref{eq:7-6})と(\ref{eq:7-7})です。

Kerasでは、Conv1D、Conv2DおよびConv3Dにおいて膨張畳込みがサポートされています。 いずれも、'dilation_rate'キーワードによって膨張率を指定することができ、 指定がない場合はデフォルトで1とみなされます。 簡単な例で膨張畳込み処理を確認しておきます。 


import numpy      as np
import tensorflow as tf
from tensorflow   import keras
from keras.layers import Input, Conv2D
from keras.models import Model
from keras        import initializers

X1 = Input(shape=(7,7,1))
Y1 = Conv2D(1, kernel_size=(3,3),dilation_rate=2,padding='same',
         kernel_initializer=initializers.Ones()) (X1)
model_1 = Model(inputs=[X1], outputs=[Y1])
モデル構成は入力層と畳込み層の2層のみです。畳込み層の引数中にキーワード'dilation_rate' を用いて膨張率を指定します。次に、モデルへの入力信号となる中央に要素１、 それ以外０の要素を持つ7x7の配列を作成・入力し、モデルの出力を得ます。確認のため、 入出力配列の次元数を印字しています。 

#入力信号の設定
x = np.zeros(49,dtype=np.int32).reshape(1,7,7,1)
x[0,3,3,0] = 1
#入力信号xに対する出力の計算
y =model_1.predict(x)

#入出力テンソルの次元数確認
print('入力テンソルの次元数：',x.shape)
print('出力テンソルの次元数：',y.shape)
x_ba,x_row,x_col,x_ch = x.shape[0:4]
y_ba,y_row,y_col,y_ch = y.shape[0:4]

print('****** 評価結果 *****')
print(y.reshape(y_row,y_col).astype(np.int32))
上記のConv2Dによる膨張率２での畳み込みは、 以下のカーネルサイズ(5x5)の標準(膨張率１)フィルタと等価なフィルタによる 畳み込みと考えることができます。この等価フィルタについては再度後述します。 

	(5x5)-標準カーネル
		1 0 1 0 1
		0 0 0 0 0
		1 0 1 0 1
		0 0 0 0 0
		1 0 1 0 1
膨張畳込み処理では、フィルタのカーネルサイズを小さく保ったままで受容野を広げることができます。 また、padding='same'として畳み込みを実行すると、入力マップ(画像)としての解像度を保ったままで、 受容野も大きくとることができます。 しかし、解像度を保ったままでの学習には多くの学習時間を必要とします。 一方、padding='same'を外すと出力マップのサイズは上下左右とも(フィルタサイズ-1) (3x3の場合２)だけ減少するため、 この効果を利用して出力画像の解像度をさげることも可能です。しかし、 入力マップ(画像)のサイズが大きい場合、この効果でサイズ縮小を図るのは現実的ではありません。 具体的に解像度を下げるためには、 何段かのPoolingレイヤーを挿入するか、strides指定を用いて解像度の縮小を図ることが必要です。

　上記で定義したネットワークモデル'model_1'はサイズ7x7の2次元配列1チャネルを入力とし、出力もサイズ7x7の1チャネル となる2次元システムと見ることができます。モデルに入力された実際のデータと、 model_1.predict()のメソッド実行によって得られた出力データの2次元配列(入出力マップ)は 以下の様になります。 


	入力マップ
		[[0 0 0 0 0 0 0]
 		 [0 0 0 0 0 0 0]
 		 [0 0 0 0 0 0 0]
 		 [0 0 0 1 0 0 0]
 		 [0 0 0 0 0 0 0]
 		 [0 0 0 0 0 0 0]
 		 [0 0 0 0 0 0 0]]
	出力マップ
		[[0 0 0 0 0 0 0]
 		 [0 1 0 1 0 1 0]
 		 [0 0 0 0 0 0 0]
 		 [0 1 0 1 0 1 0]
 		 [0 0 0 0 0 0 0]
 		 [0 1 0 1 0 1 0]
 		 [0 0 0 0 0 0 0]]
入力配列の中央にのみ'1'、それ以外0の要素値を持つデータは、2次元システム'model_1' に対する2次元インパルス信号であると言えます。 2次元システムにインパルス信号を入力した場合の出力はシステムのインパルス応答と呼ばれます。 任意の入力信号に対するシステムの出力は、 このインパルス応答信号と入力信号との畳込み積和によって得られます。 従って、上の出力マップはインパルス応答そのものですので、 膨張率を指定した場合の畳込み層(ネットワークシステム)のインパルス応答を表しています。 この出力マップの最外郭列(行)は全て0ですので、それらを除いた(5x5)行列をカーネルとして持つ 標準の畳込みフィルタと解釈することができます。

文脈情報の多重化

　濃密予測の効率化を図る場合、文脈情報を多重化して収集することが有効です。 様々な種類の文脈情報が考えられますが、この節で扱う文脈情報は受容野を変化させた場合の 畳込み演算による特徴マップを対象とします。前述したように、膨張畳込みでは物理的な解像度を 下げることなく、受容野を拡大した特徴マップを作成することができます。 従って、膨張率を変化させて膨張畳込み処理を行い、その結果を直接マージすることで、 文脈情報の多重化が可能となります。 文脈の多重化について述べる前に、モデルの各層を表すパラメータの扱いについて簡単に触れます。 学習を行わずに所望の畳込みフィルタを得ようとすると、モデル定義の段階で初期値として パラメータを設定する必要があります。この初期値設定に必要な情報の確認から入ります。 フィルタのパラメータは2種類のデータ、 すなわちカーネルの各要素の係数（重み）と活性化関数の閾値で構成されています。 以下のKerasを利用した簡単なモデル定義の例について考えます。 

import cv2
import numpy      as np
import tensorflow as tf
from tensorflow   import keras
from keras.layers import Input, Conv2D, Concatenate
from keras.models import Model
from keras        import initializers
from matplotlib   import pyplot as plt

X0 = Input(shape=(256,256,1),name='input')
X1 = Conv2D(64,(3,3),padding='same',name='conv_1')(X0)
X2 = Conv2D(1, (1,1),padding='same',name='conv_2')(X1)
model_2 = Model(inputs=[X0], outputs=[X2])
model_2.summary()
と入力すると、以下のような結果が出力されます。 

Model: "model_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
input (InputLayer)           (None, 256, 256, 1)       0
_________________________________________________________________
conv_1 (Conv2D)              (None, 256, 256, 64)      640
_________________________________________________________________
conv_2 (Conv2D)              (None, 256, 256, 1)       65
=================================================================
Total params: 705
Trainable params: 705
Non-trainable params: 0
_________________________________________________________________
改めて各層のパラメータ数について補足すると、 ネットワークの０層は入力層であり、パラメータ数は０個です。１層は 'conv_1'と名づけられたConv2D層で、この層に割り当てられたパラメータ数は 640個です。3x3のカーネルによる畳込みを表すのに必要な3x3x1の係数と、 畳込み後の結果に対する活性化関数の閾値が1個、 すなわち1フィルタ当たり合計9+1=10個のパラメータが必要です。同様のフィルタを64個確保する のに必要な総パラメータ数は、(9+1)x64=640となります。 レイヤークラスに定義されているメソッドget_weights()を用いることで、 これらのパラメータの具体的な内部表現を知ることができます。 すなわち、 

L1 = model.layers[1]
W1 = L1.get_weights()
print(W1[0].shape)
print(W1[1].shape)
によって取り出されるのは、レイヤー１内のフィルタの重み係数と 活性化関数の閾値のリストです。重み係数については、 カーネルサイズ(row,col)、デプス(depth)、フィルタ総数(filters))の大きさを持つ 4次元numpy型配列として表されています。一方、閾値については1次元numpy型配列として表現されています。 従って、print()関数によって表示されるそれぞれの配列の構造は、以下のようになります。
(3,3,1,64)
(64,)
レイヤー１のConv2D層では、カーネルサイズ3x3の大きさを持つ畳込みフィルタが64個分、 また活性化関数の閾値もフィルタ数分だけ確保されていることが分かります。 レイヤー２も畳込み層ですが、カーネルサイズは１ｘ１であり、入力マップ内での畳込み効果はありません。 代わりに入力マップのチャネル間の積和をとります。この層についても、重み係数の内部表現構造を求めてみます。 

W2=model.layers[2].get_weights()
print(W2[0].shape)
print(W2[1].shape)
を実行した結果は、
(1,1,64,1)
(1,)
となります。これで、 フィルタの初期値データの表現構造について確認することができました。

　以上の内容を踏まえ、画像処理でよく用いられる3x3のラプラシアンフィルタを畳込み層の中に 作成します。即ち、ラプラシアンフィルタとして用いられる3x3のマスクの各要素を、numpy型4次元配列'kernel_0' として与えます。 また、異なるdilation_rateで膨張畳込みを行った結果を統合するための1x1の畳込み層の初期値を 同じくnumpy型4次元配列'kernel_1'として定義します。 ここでは、それぞれの膨張畳込み結果を均等に統合する重み係数とします。 


#######   入力画像の設定と読込   #######
img_path ='sample1.pgm'          
x = cv2.imread(img_path,0)       #画像の読み込み(白黒階調画像)
x = x/255.0                      #画素値を[0,1]に正規化
x = x.reshape(*x.shape,1)        #チャネル情報を追加

#######  畳込み層の重み係数設定  #######
kernel_0 = np.array([1,1,1,1,-8,1,1,1,1]).reshape(3,3,1,1)
kernel_1 = np.array([1,1,1,1]).reshape(1,1,4,1)

####### ネットワークモデルの定義 #######
X0 = Input(shape=(x.shape))
X1 = Conv2D(1,(3,3),padding='same',name='conv_1',dilation_rate=1,
            kernel_initializer=initializers.Constant(kernel_0))(X0)
X2 = Conv2D(1,(3,3),padding='same',name='conv_2',dilation_rate=2,
            kernel_initializer=initializers.Constant(kernel_0))(X0)
X3 = Conv2D(1,(3,3),padding='same',name='conv_3',dilation_rate=4,
            kernel_initializer=initializers.Constant(kernel_0))(X0)
X4 = Conv2D(1,(3,3),padding='same',name='conv_4',dilation_rate=8,
            kernel_initializer=initializers.Constant(kernel_0))(X0)
Y0 = Concatenate()([X1,X2,X3,X4])
Y1 = Conv2D(1,(1,1),padding='same',name='bottle_neck',
			kernel_initializer=initializers.Constant(kernel_1))(Y0)

M = []                           #モデルのリスト表現
M.append(Model(inputs=[X0], outputs=[X1]))
M.append(Model(inputs=[X0], outputs=[X2]))
M.append(Model(inputs=[X0], outputs=[X3]))
M.append(Model(inputs=[X0], outputs=[X4]))
M.append(Model(inputs=[X0], outputs=[Y1]))

###### 畳込み処理の実行と出力表示 ######
x = x.reshape(1,*x.shape)        #バッチ数１を設定
y = []
for i in range(5):
    y.append(M[i].predict(x))    #各モデルの予測実行

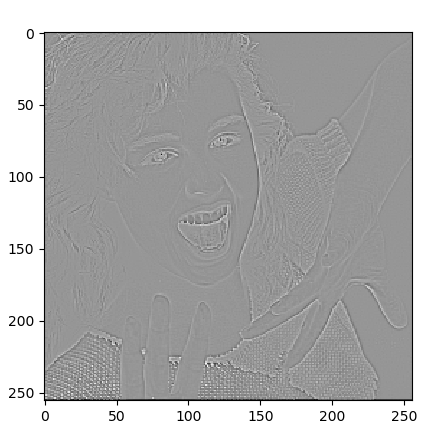
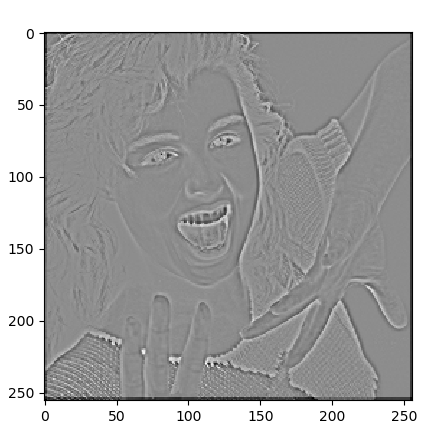
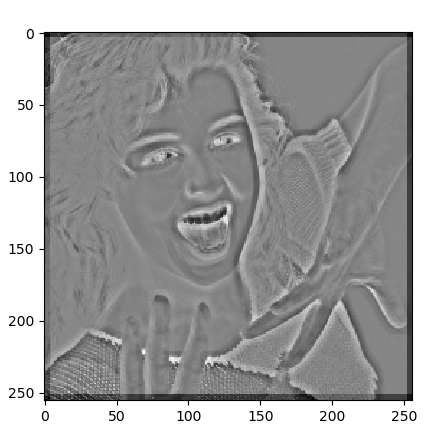
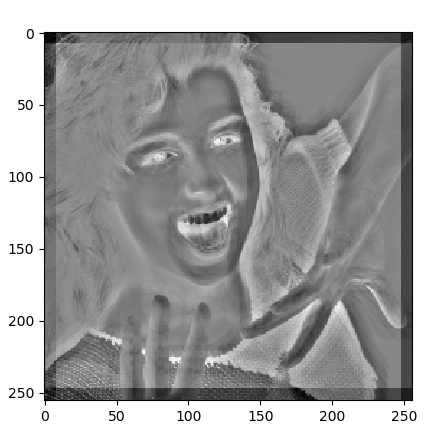
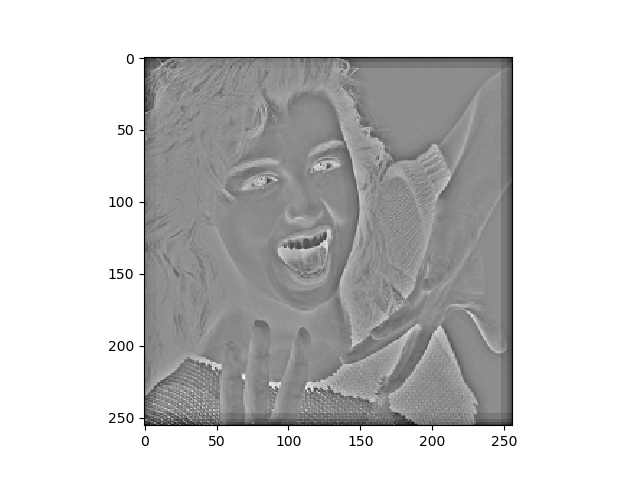
for i in range(5):               #各予測結果の画像表示
    z = y[i].reshape(y[i].shape[1:3])
    plt.imshow(z,cmap='gray')
    plt.show()
########### 多重化処理の終了 ###########
上記のプログラムでは、膨張係数が１，２，４，８の畳込みを行う４つのネットワークモデル を定義し、それらの各出力を１つの特徴マップに連結したうえで1x1の畳込み層へ引き渡して います。図7-2は、４つのモデルからの出力を可視化した結果です。膨張係数が異なる４つの ラプラシアン画像を等しい重みで１つのマップに多重化した結果が図7-3の画像です。 なお、実験に利用した画像は白黒階調画像ですが、カラー画像の場合には入力チャネル数、および フィルタ係数の初期値を変更する必要があります。

図7-2 膨張畳込み処理の例(dilation_rate=1,2,4,8)

図7-3 膨張畳込み画像の多重化処理の例

参考資料